CZGM and CZGM-iso
The CZGM is written in Matlab. The user needs to install first the MATLAB software (Version R2016b or higher) in her/his computer.
The detailed procedure of the program can be found in the folder CODE in the file CZGM_description.m which can be open in Matlab or in a notepad as a txt file.
The CZGM-iso is a modified version, which uses a concentration of the initial profile from the calculated isopleths by Werami. Detail of the procedure can be found in the attached manual (CZHM-iso-manual)
CZGM combines pseudosection modelling using Perple_X and multicomponent diffusion in garnet during metamorphism. It uses the initial compositional profile, obtained by Perple_X with the application of garnet fractionation, to generate a population of garnets of prescribed size-distribution and to apply multi-component diffusion along a selected PT path during prograde metamorphism and subsequent decompression and/or cooling. As an example, CZGM was applied on average pelitic rocks subjected to metamorphism at different temperatures (600 to 800 °C) and time duration of 1-10 Ma. CZGM provides an easy-to-handle tool for petrologists to examine hypothetical scenarios of garnet development along prograde and retrograde paths and to constrain the PT path of metamorphic processes. By treatment of laboratory-measured garnet-bearing metamorphic rocks, it allows to improve the accuracy of pressure and temperature conditions, usually estimated only from compositional isopleths of garnet.
A detailed description of the components of CZGM, its folders, files and functions can be found in the file CZGM_description.m. Here we provide the parts concerning the garnet formation, multicomponent diffusion and an example of modelling sequence.
1. Garnet formation (function make_garnets)
The function make_garnets takes information about fractionation along the selected PT-path to model a population of garnets that are created and grow gradually along the PT-path so that they, in the end, reach a prescribed size-distribution. It implies that nucleation of garnet is modelled as an episodic process that is controlled not only by the fractionation data but also by an assumption about size-distribution. The procedure is similar although technically not identical to Gaidies et al. (2008). A user defines garnet size distribution by means of a function f(r) that is then discretized from rmin to rmax into a number of classes which defines also constant radius increment dr. Garnets are approximated by spheres increasing by shells of thickness dr. From a previous run of the function run_vertex, the function make_garnets takes the amount of garnet volume accumulated along the PT-path as a function of relative time, GV(t). This function is normalized to 1, i.e., it goes from a small volume GV at the PT-point where vertex predicted the first appearance of garnet, to GV=1 at the PT-point where the garnet formation stopped. Script make_garnets run a cycle through all size-classes. For each size-class of garnet, a point on the cumulative GV(t) curve is found where the volume increase is sufficient to feed a newly created class and to increase all existing classes by new shells of thickness dr. This procedure ensures that, at the PT-point where garnet formation stops, all size-classes are built proportionally to the required size-distribution. The assignment of formal (relative) time to the classes allows also to assign the corresponding P, T and modal composition to individual shells in each garnet. The growth of all garnet classes is tracked graphically but only information about garnet whose diffusional relaxation user intends to model subsequently (by means of the function make_diffusion) is kept by the end of the run of make_garnets and passed to global variables. This garnet must be specified by a user before running make_garnets by setting the parameter garnet_no equal to the class-number where the garnet belongs. The parameter garnet_no is predefined already in the initial_setup, but can be changed ad hoc from the command line anytime before running make_garnets. On the output, the function make_garnets provides profiles of garnet composition (variables Fer, Mnr, Mgr, Car and corresponding time tr) altogether with information about the time remaining to go along the PT-path after garnet stopped its growing. These data will be used in make_difussion.
2. Multicomponent diffusion (function make_diffusion)
Multicomponent diffusion in garnet is modelled using the Fick’s–Onsager approach (Onsager, 1945) as a coupled system o three diffusion equations. In spherical coordinate system fixed in the centre of garnet the equations have the form
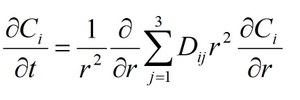
where indices ![]() correspond to the concentrations of Fe, Mg, and Mn (independent components) while the concentration of Ca (dependent component) is given as C4 = 1-C1-C2-C3. Equations are solved numerically by means of a finite difference method. Diffusion coefficients
correspond to the concentrations of Fe, Mg, and Mn (independent components) while the concentration of Ca (dependent component) is given as C4 = 1-C1-C2-C3. Equations are solved numerically by means of a finite difference method. Diffusion coefficients ![]() depend on tracer diffusion coefficients
depend on tracer diffusion coefficients ![]() according to (Lasaga, 1979).
according to (Lasaga, 1979).
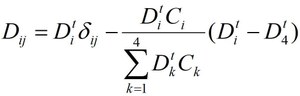
where ![]() is Kronecker’s delta. The application of diffusion on a garnet consists of two parts. First, the function make_diffusion follows, step by step, the garnet growth computed and recorded previously in make_garnets and at each step, it runs diffusion in the actual garnet for time interval dt=tr(i)-tr(i-1). Dirichlet boundary condition is applied at the outermost node keeping constant concentrations of Fe, Mn, Mg, and Ca on the garnet rim. Second, when garnet is completed, diffusion continues along the remaining PT-path until its end. The boundary condition for this part is optional and can be set from the command line by means of the parameter BC. There are 3 possibilities: BC=0 – keep constant concentrations of the elements on the garnet rim; BC=1 - user-supplied boundary concentrations; BC=2 – insulated garnet (closed system with zero gradients on the rim); BC=3 – boundary concentrations of Fe and Mg are interpolated from PT-grids (files Fe.tab, Mg.tab) at points of the remaining PT-path, while the concentration of Mn=0, and Ca=1-Fe-Mg. Besides the options for boundary conditions, the function make_diffusion provides also several options for diffusion coefficients that are available via the parameter diff_mode (diff_mode=1 for Chakraborty and Ganguly, 1992; 2 for Carlson, 2006; 3 for Vielzeuf, 2007).
is Kronecker’s delta. The application of diffusion on a garnet consists of two parts. First, the function make_diffusion follows, step by step, the garnet growth computed and recorded previously in make_garnets and at each step, it runs diffusion in the actual garnet for time interval dt=tr(i)-tr(i-1). Dirichlet boundary condition is applied at the outermost node keeping constant concentrations of Fe, Mn, Mg, and Ca on the garnet rim. Second, when garnet is completed, diffusion continues along the remaining PT-path until its end. The boundary condition for this part is optional and can be set from the command line by means of the parameter BC. There are 3 possibilities: BC=0 – keep constant concentrations of the elements on the garnet rim; BC=1 - user-supplied boundary concentrations; BC=2 – insulated garnet (closed system with zero gradients on the rim); BC=3 – boundary concentrations of Fe and Mg are interpolated from PT-grids (files Fe.tab, Mg.tab) at points of the remaining PT-path, while the concentration of Mn=0, and Ca=1-Fe-Mg. Besides the options for boundary conditions, the function make_diffusion provides also several options for diffusion coefficients that are available via the parameter diff_mode (diff_mode=1 for Chakraborty and Ganguly, 1992; 2 for Carlson, 2006; 3 for Vielzeuf, 2007).
3. Modelling sequence (CZGM_script)
% CZGM_script
% Compositional Zoning in Garnet and its Modification by diffusion (CZGM)
% Modelling with CZGM consists of the following steps
% (see the functions CZGM_description and initial_setup for details)
% (0) Preparation and initial setup
initial_setup
% (1) Design of PT-path make_path % (2) Fractionation along PT path
run_vertex
% (3) Formation of garnet population
make_garnets
% (4) Assignment of time to PT path
make_time
% (5) Multicomponent diffusion in a chosen garnet
make_diffusion
% User can run the whole sequence of steps, or run steps 1,2 and then repeatedly 3 and 5 with different choice of garnet-size and subsequent diffusion, or repeat diffusion, step 5, with different time setup.
Modelling steps illustrated by figures:
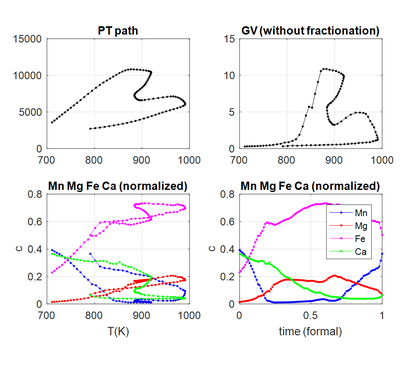 Fig. A2. Interpolated concentrations of basic garnet elements provide a first insight.
Fig. A2. Interpolated concentrations of basic garnet elements provide a first insight.
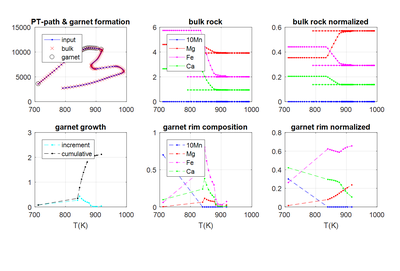 Fig. A3. Result of fractionation is analyzed and pre-processed for subsequent garnet formation.
Fig. A3. Result of fractionation is analyzed and pre-processed for subsequent garnet formation.
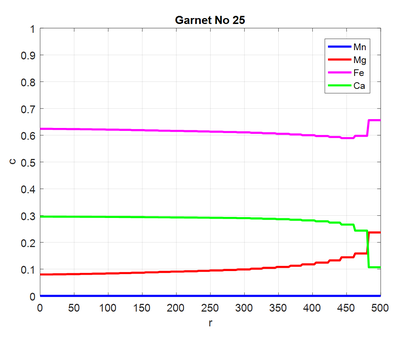 Fig. A4. Population of garnets is created and one its members is prepared for diffusion.
Fig. A4. Population of garnets is created and one its members is prepared for diffusion.
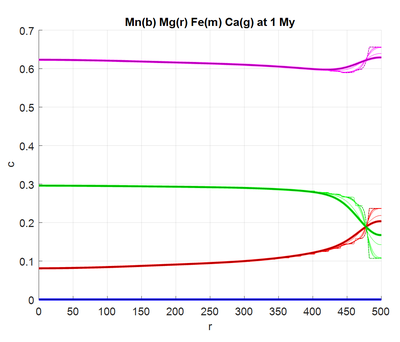 Fig. A5. Diffusion is applied to concentration profiles over defined time and with prescribed boundary conditions.
Fig. A5. Diffusion is applied to concentration profiles over defined time and with prescribed boundary conditions.
Download CZGM -iso-ini software here
Download CZGM -iso-dif software here
Download CZGM -iso manual here
Download CZGM -vertex software here
Document Actions